Bayesian designs are particularly suited for early drug development as they combine historical information with current trial data to make decisions on toxicity, efficacy or futility.
Early clinical drug development is targeted at gathering information about the toxicity and efficacy of a new drug compound. Phase I trials determine the maximum tolerated dose of a drug while Phase II trials explore efficacy and lead to a critical decision of go-no-go in terms of continuing a drug’s clinical program. Bayesian designs are particularly suited for early drug development as they combine historical information with current trial data to make decisions on toxicity, efficacy or futility.
Traditional designs, e.g. parallel group, have long been the mainstay of clinical trials. These designs are appealing because they are rigorous, robust and focussed. Yet at the same time, these desirable qualities often place limits on innovation and analysis. Some limitations include:
• Inflexibility; design parameters cannot be changed without affecting robustness
• Inability to focus on single therapeutic agents
• Employ different endpoints in Phase II (short-term) vs. Phase III (long-term)
• Restriction on statistical inferences to information in the current trial
Traditional designs are more appropriately suited to Phase III studies. However, during early drug development, more innovative designs that allow effective decision- making are needed and by doing so, overall drug development time may be reduced.
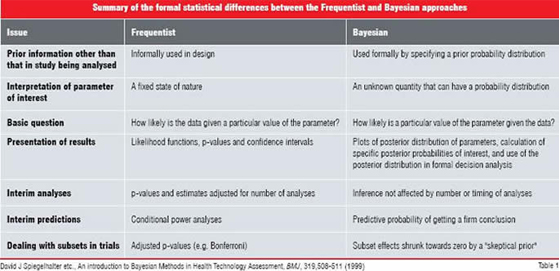
In statistics, there are two schools of thought—Frequentist and Bayesian. Most traditional designs have their roots in Frequentist statistics and although one may or may not be aware of it, when we employ terminology such as "confidence intervals" and "p-values", we are describing Frequentist characteristics of data. Bayesian statistics is based on a theorem known as “Bayes Theorem”. This theorem provides a method for updating historical or prior information with current information to determine if a hypothesis is true. In contrast, the Frequentist approach ignores any historical or prior information and all inferences are based on the observed data.
The objective of a Phase I study is to determine the maximum tolerated dose (MTD) of a new drug compound that produces a specified level of toxicity. The traditional design for a Phase I study has often been the “1-in-3”, “3+3” design or variations thereof. The approach is deterministic in nature and one variation is described as follows:
• Treat 3 patients at the starting dose level Di
• If 0 patients experience dose-limiting toxicity (DLT), escalate to dose Di+1
• If 1 or more patients experience(s) DLT, treat 3 more patients at dose level Di
• If 1 of 6 experiences DLT, escalate to dose Di+1 • If 2 or more experience DLT, MTD = Di-1 Dose escalation stops when 1/3 patients (33%) have DLT at a given dose level; MTD is the next lower dose level. Although inherently simple to use, this approach has several limitations:
• Inability to account for indication or patient populations with specific dose limiting toxicity rates
• Dose levels need to be defined in advance
• Sample size is variable
• Confidence in the chosen MTD is poor
• Difficult to modify for different DLT rates
The Continual Reassessment Method (CRM) introduced by O’Quigley, Pepe and Fisher (1990) provided the first formal ‘statistical’ approach to determining the MTD. The method is Bayesian in nature and allowed the MTD to be determined with continually updated data. The method is described as follows:
• Determine the range of doses to be explored
• Assign a probability of toxicity to each dose based on historical data or investigator input; this represents prior information and is the starting point for the search
• Define a model that represents the doseresponse relationship; e.g. a tangent hyperbolic or other logistic regression model
• Treat patients at the starting dose
• Observe dose-limiting toxicities
• Calculate the next best estimate of the MTD based on the prior information and the current results of the study
Based on this approach, patients are treated at the dose at which currently available evidence indicates to be the best estimate of the MTD. The CRM is flexible and allows different number of patients to be treated per dose and could target a preselected dose limiting toxicity rate.
Phase I designs usually involve a single administration of the drug. However, in some situations, investigators may administer a drug repeatedly and monitor long-term effects of toxicity. In these cases, the objective of the trial may not be to determine the MTD but rather the maximum tolerated schedule (MTS) of a drug. Braun et al. (2005) proposed a new method for this setting.
The proposed method uses patient’s time to toxicity as the outcome, with the hazard of toxicity modelled as the sum of a sequence of hazards, each associated with one administration. The MTS that the patient may receive is based on the risk of toxicity occurring within a specified follow-up period that includes the maximum schedule being considered. Patient accrual, data monitoring, and outcome-adaptive decision making are done continuously throughout the trial under a Bayesian formulation. Each time a new patient is accrued, the most recent data is used to evaluate criteria that defines the optimal schedule, which is assigned to the new patient.
Thall et al.(2004) extended the Phase I paradigm to include not just safety, but also efficacy. Their argument was that Phase I design is too limited and ignores several important factors:
• Response. No patient hopes only for “No toxicity”
• Assumes that the probability of response is monotone with dose
• May be inefficient when the probability of toxicity is low for all doses but that the probability of response increases with dose. In this case, the superior higher dose may not be found.
The approach of Thall et al. combines the objectives of Phase I and Phase II trials. Patient outcome in the trial is a bivariate outcome consisting of the possible set of outcomes for toxicity and for response and like the CRM method the efficacy-toxicity tradeoff method is Bayesian in nature.
The investigator would define the following:
• lowest acceptable level of response
• highest acceptable level of toxicity
• three equally desirable levels of response, toxicity
The three desirable targets, ?1 *, ?2 * and ?3 * set up the initial efficacy-toxicity tradeoff contours (dimension reduction). The first target, ?1 *, represents the minimum probability of efficacy when toxicity is not expected (i.e. probability of toxicity = 0) while ?2 * is the maximum probability of toxicity when efficacy is certain (i.e. probability = 1). The final target ?3 * is an intermediate point between the smallest efficacy and largest toxicity probabilities. These construct the target contour C as in Figure 1 (Thall & Cook, 2004). As illustrated in Figure 1, ?1 * is (0.15, 0), ?2 * is (1.0, 0.55) and ?3 * is (0.25, 0.30).
The contour C is then used to define desirable probabilities for any pair of probabilities q which in turn determines the desirability of the doses under investigation. A family of trade-off contours can then be constructed (see Figure 1). Once this structure has been defined, the dose-finding algorithm is as follows:
1. Investigator chooses the starting dose
2. Dose x is acceptable if the dose has acceptable probabilities of efficacy and toxicity or if the dose is the lowest untried dose and has an acceptable probability of toxicity
3. Treat each group of subjects at the current most desirable dose
4. Do not skip untried doses
5. If no dose is acceptable, stop the trial
6. At the end of the trial, select the most desirable dose
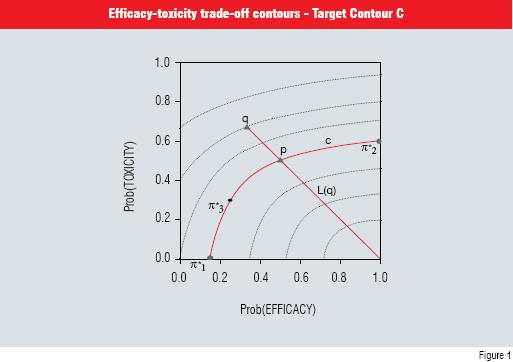
Figure 1 Efficacy-toxicity trade-off contours. The three elicited target points that determine the target contour C are given by round dots. The two triangular points illustrate the desirability of any pair of probabilities
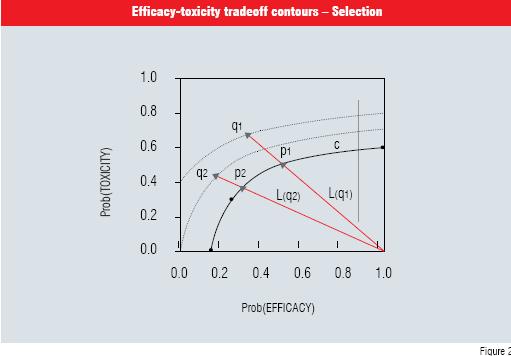
Figure 2 illustrates the selection process with 2 pairs of points, q1 and q2. The point q2 is more desirable because its contour is closest to the desired C contour.
Two key advantages to this approach are: (i) the method reliably finds safe doses with high efficacy and (ii) stops if no dose is acceptable.
The proof-of-concept study represents another area that is an ideal target for innovative designs. Proof-of-concept studies are carried out to determine if there is early evidence of clinical efficacy using a small, targeted number of subjects, to warrant taking a drug further into development. Traditional designs may not be appropriate for a number of reasons: designs with a placebo arm may be unethical, designs are based on a fixed sample size and conclusions can only be drawn once the study is completed, etc. Designs that address these limitations include twostage Simon designs, three-stage designs, optimal flexible two-stage designs and adaptive two-stage designs. As their name suggests, the study is implemented in stages. At each stage, the data from subjects in the study are examined and a decision is made to stop the study early or to enroll additional subjects into the next stage.Adaptive designs refer to designs in which the design factors can be adjusted during the trial. Design factors that can be adjusted include sample size, dropping ineffective treatment arms, randomisation, stopping early rules, etc. The decision is usually based on accumulating data in the current trial but can also accommodate data from other ongoing trials. The Continual Reassessment Method is an example of an adaptive design. Other Bayesian examples can be found in articles by Thall, Sung & Estey (2002) and Thall & Wathen (2005). In the latter paper, the study was designed to address patient heterogeneity (covariates) and multi-stage therapies.
Benefits of adaptive designs include reduction in sample size, the ability to assess predictive probabilities of statistical significance and terminate early if there is no evidence of drug effect, reduction of total drug development time and the availability of long term safety data earlier.
Innovative designs such as those described in this article present valid, efficient alternatives to traditional designs typically used in early drug development. The Bayesian approach seems ideally suited to early phase trials for the following reasons:
• borrows strength from combining historical/ prior information with accumulating data
• supports model-based estimation, thereby improving efficiency
• has practical applications in situations where it is necessary to make design changes; e.g. covariate adaptive randomisation
• naturally provides an ideal framework for decision making, as opposed to hypothesis testing.
1. Spiegelhalter, DJ. An Introduction to Bayesian Methods in Health Technology Assessment, BMJ, 319, 508-511 (1999).
2. O’Quigley, J., Pepe, M., and Fisher, L... Continual reassessment method: A practical design for Phase 1 clinical trials in cancer. Biometrics;46, 33–48 (1990)
3. Braun T, Yuan Z, Thall P. Determining the maximum tolerated schedule of a cytotoxic agent. Biometrics, 61, 335 (2005)
4. Thall, PF, Cook, J. Dose-finding based on toxicity-efficacy trade-offs. Biometrics; 60, 684–693 (2004).
5. Simon, R. Optimal two-stage designs for phase II clinical trials. Controlled Clinical Trials, 10:1-10, (1989).
6. Thall PF, Sung H-G, Estey EH. Selecting therapeutic strategies based on efficacy and death in multi-course clinical trials. J American Statistical Assoc, 97:29-39 (2002.).
7. Thall PF, Wathen JK. Covariate-adjusted adaptive randomization in a sarcoma trial with multi-stage treatments. Statistics in Medicine, 27:1947-1964 (2005).