The development of solids-based pharmaceutical manufacturing has been facilitated by the use of process modelling and simulation-based process analysis methods. Such in silico approaches are implemented to efficiently predict process behaviours, identify critical process parameters, and quantify the process design space, that contribute to an enhanced process understanding.
In recent years, the pharmaceutical industry has been actively involved in exploring advanced manufacturing processes that can help reduce the manufacturing costs and improve the product quality. One of the most promising route is the switch from batch to Continuous Pharmaceutical Manufacturing (CPM) processes. The continuous production mode enables a steady-state operation, where product quality exhibits only low variability over time. Therefore, a well-designed CPM process can result in improved product quality and uniformity. In addition, since a CPM process usually requires fewer steps than a batch process, it also helps to reduce capital and operation costs, which lead to a better economic efficiency.
A successful implementation of a CPM process requires to fully understand how different material properties and operations conditions can jointly affect the process behaviour and product attributes. Process modelling can facilitate this step and be used to store this knowledge. By applying modelling techniques to pharmaceutical manufacturing processes, we can achieve a better process understanding with only a limited number of experiments. A welldeveloped and validated process model can be utilised to further understand the process dynamics and moreover to efficiently transfer this knowledge. The objective of this paper is to present a variety of modelling approaches that have been developed in our lab in the last decade for solids-based CPM process, as well as how to use the models in a systematic manner to enrich the process understanding.
The difficulties of modelling the solids-based pharmaceutical processes mainly result from the complexity of the particle-level and bulk behaviours of material flows. To address such difficulties, the Discrete Element Method (DEM) approach has been used for modelling various pharmaceutical processes. The DEM tracks the motion and positions of each particle individually, which then provides a huge amount of detailed information of the dynamics of particles. This information is usually hard to be obtained directly form physical experiments, but can be crucial to the investigation of particlelevel phenomena (e.g., segregation, agglomeration). However, the DEM simulations are computationally intensive and can only be applied to systems with a limited number of discrete particles.
The Population Balance Models (PBMs) describe the time-dependent properties for a group of entities using a set of partial differential equations which involve the mass, momentum, and energy balance for the systems of interest. The term ‘entities’ are referred to particles whose states are described by a vector containing both internal coordinates (e.g., particle size, mass) and external coordinates (e.g., physical locations). Multidimensional PBMs have been used to model pharmaceutical processes with various internal coordinates (e.g., particle size, porosity, composition). However, they require a high computational cost to evaluate the model. Recently, hybrid models combining DEM simulations and PBMs have been developed to describe pharmaceutical processes such as granulation, milling, and mixing.
Data-driven models (sometimes known as Reduced Order Models) are an efficient approach to investigate the system input-output relationship when first-principle models are not available or too expensive to be obtained. A broad range of modelling techniques can be categorised as a data-drive approach. Response Surface Methodology (RSM), probably the mostly used regression technique, describes the process with a low-degree polynomial model. A RSM model is usually constructed based on physical experiments using a Design of Experiment (DoE) sampling plan. Partial Least Squares (PLS) regression is a multivariate regression approach which projects the dataset to a lowerdimensional latent space where the correlation between process inputs (X) and outputs (Y) are maximised. The PLS approach is especially useful to analyse high-dimensional and noisy data with strong collinearities between X and Y. Artificial Neural Network (ANN) is a modelling technique inspired by the way that human brain processes information. An ANN network consists of a number of single units (known as “neurons”) which are interconnected with coefficients (i.e. weights). The numerous ways of connecting different units constitute the foundation of the flexibility of the ANN models. Kriging models a process output as the realisation of a Gaussian process, of which the errors are assumed to be spatially correlated. The Kriging model has the advantage of providing both the best linear predictor and the estimated prediction error, which are useful to evaluate the accuracy of the prediction and decide future sampling directions. Kriging is a powerful approach to approximate expensive simulations which have complex and nonlinear surfaces.
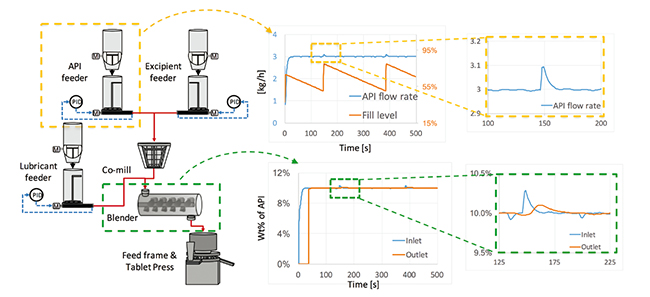
Models for unit operations are the basic elements for understanding a process. At the Center for Structured Organic Particulate System (C-SOPS), a complete (and constantly being improved) model library has been developed for all the major unit operations of continuous pharmaceutical manufacturing processes, including feeding, mixing, milling, tableting, etc. Such models are implemented on a gPROMS simulation platform. On the basis of these models, flowsheet models can be developed as an approximation of the plantwide manufacturing process. In a flowsheet model, unit operation models are connected with flow information being transferred between consecutive processing steps. As such, the process responses to the change in operations (or material variations) can propagate along the process, which can be predicted by the flowsheet model. This is demonstrated with Figure 1. The flowsheet of a Continuous Direct Compaction (CDC) process is shown on the left in Figure 1, where two raw materials (i.e., Active Pharmaceutical Ingredient (API), excipient) are fed to a co-mill for the purpose of de-lumping, after which the mixtures together with a lubricant, are transferred to a blender for mixing. The blends are sent to the press where tablet products are continuously produced. The dynamics of the process predicted from the flowsheet model are shown on the right in Figure 1. The top two charts show the flow rate and fill level of the API feeder. We can notice that as the feeder runs, refilling of the materials is needed, which can cause temporal variations to the flow rate. In the bottom two charts, the propagation of such variations after the blender is predicted. It can be observed that after mixing the variations in the API composition are dampened to a much smaller level. Such predictions are useful in choosing the best refilling strategy that leads to products with desired quality attributes.
A developed flowsheet model can be used to interrogate the process behaviour as illustrated in the previous section and provide invaluable information regarding risk analysis and process design space as will be described in this section.
For a complex model with many input variables (X), it is usually the case that only a small subset of such variables has a huge impact on the process outputs (Y) of interest. Such influential model inputs can be identified by the Global Sensitivity Analysis (GSA). Formally, GSA investigates how uncertainties in X can contribute to variations in Y over the whole input space. Compared to local sensitivity methods which are based on calculating elementary effects around a single nominal point, GSA methods are based on space-filling sample points, and can reveal both the main effects and high-order interaction effects of X on Y.
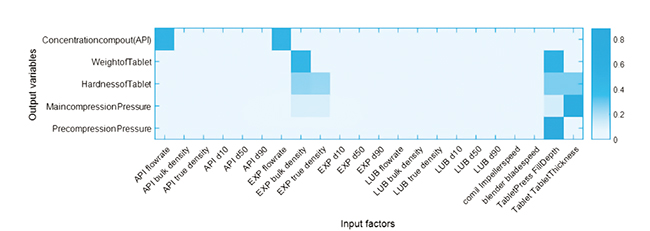
Figure 2 Intensity plot of the global sensitivity analysis result (22 input factors and 7 output variables)
Various GSA methods have been developed for different engineering problems. In practice, when the sampling budget is limited, a more effective way is to first use a fast screening method (e.g., Morris method) followed by a more computationally costly variancebased method (e.g., Sobol’ method). The screening method usually requires a much smaller number of sampling points and can be efficient in prioritising input factors by qualitatively comparing their influence on the outputs. After the results are obtained, the less important variables can be fixed at their nominal values, while the remaining input factors are analysed using the variance-based method. Although the variance-based method can require more sampling points, detailed information can be obtained to quantitatively examine the percentage of variance in Y that is apportioned to a certain input factor.
To demonstrate the use of GSA, we show a case study of a CDC process in Figure 2. In this example, we investigate how the 22 input factors (horizontal axis), including operation conditions and material properties, can affect the variations in 5 output variables (vertical axis), including product attributes and process responses. The sensitivity information is visualised with an intensity plot: the darker the colour block, the more sensitive the input factor. From the results, we can see that only 6 input factors (i.e., API flow rate, Excipient flow rate, Excipient bulk density, Excipient true density, tablet die fill depth, tablet thickness set point) have a critical influence on the 5 output variables of interest. The results indicate that, when operating the process, controlling strategies should focus on the 6 most influential input factors in order to reduce the variability in the process outputs.
In pharmaceutical processes, the GSA methods have been successfully applied to reduce the dimensionality of a complex flowsheet model. The results are important to identify critical process parameters and provide guidance to the development of control strategies.
To ensure the consistency of product quality, it is important to evaluate the process design space, which is defined as “the multidimensional combination and interaction of input variables and process parameters that have been demonstrated to provide quality assurance” according to the document “Guidance for Industry, Q8 Pharmaceutical Development” by Food and Drug Administration (FDA). The design space can be mathematically defined via the use of feasibility analysis.
The objective of feasibility analysis is to quantify the feasible region within which all the process constraints are met. Mathematically, feasibility can be defined as the maximum violations of all the constraints: ?(?)= max-(j?J) {g_j (?)}. As such, the feasibility analysis problem is to identify the region where ?(?)=0.
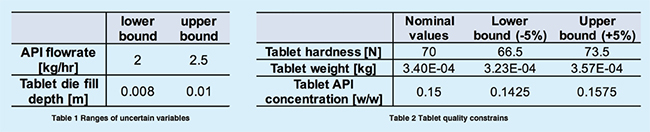
In our group, we have developed an efficient approach called “surrogatebased feasibility analysis” to characterise the design space for pharmaceutical processes. The advantage of this approach is to accurately predict the design space with the smallest sampling budget. This is demonstrated with the following case study. On the basis of a developed tablet press model, our objective is to find the design space within the ranges of uncertain parameters (i.e., API flow rate and Tablet die fill depth) in Table 1, that will result in the qualified tablets with properties (i.e., hardness, weight, API composition) within the specified ranges in Table 2.
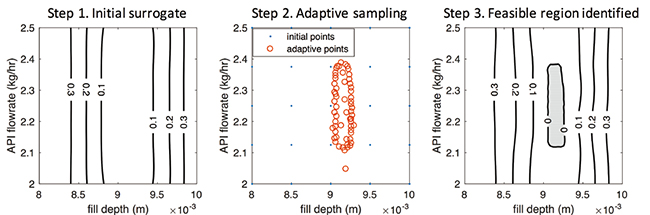
The surrogate-based feasibility analysis solves this problem in the following 3 steps (Figure 3). First, an initial low-fidelity surrogate model is built with a small number of space-filling sample points obtained by running the tablet press model. Then, adaptive sampling is performed to iteratively sample where it is more likely to be the design space boundary. At each iteration, the knowledge of the actual design space is improved, and the accuracy of the surrogate model also gets updated. Finally, when the sampling budget is depleted, the highly accurate prediction of the design is returned by the surrogate model, which is shaded in the grey area in Figure 3. Therefore, in order to produce qualified tablet products, the operation conditions should be controlled within this shaded design space: 9.05= fill depth [mm] =9.25 n2.1=API flow rate [kg/h]=2.4. Any combination of operations out of this region will cause violations of at least one of the quality constraints in Table 2.
In this article, we have discussed different modelling techniques that have been used to study solids-based continuous pharmaceutical manufacturing processes. The capabilities of flowsheet models to predict process dynamic behaviours are demonstrated with an example of a direct compaction process. Further applications of flowsheet models include global sensitivity analysis and feasibility analysis, which are extremely beneficial in identifying critical process parameters and characterising the process design space. Future work is focused on improving the current models with additional experiments, and extending the current model-based process analysis framework to other continuous manufacturing processes.
Acknowledgment:
The authors would like to acknowledge financial support from FDA (DHHS - FDA - 1 U01 FD005295-01) as well as National Science Foundation Engineering Research Center on Structured Organic Particulate Systems (NSF-ECC 0540855).
References:
1. Rogers A J, Hashemi A, Ierapetritou M G. Modeling of particulate processes for the continuous manufacture of solid-based pharmaceutical dosage forms[J]. Processes, 2013, 1(2): 67-127.
2. Ketterhagen W R, am Ende M T, Hancock B C. Process modeling in the pharmaceutical industry using the discrete element method[J]. Journal of pharmaceutical sciences, 2009, 98(2): 442-470.
3. Ramkrishna D, Singh M R. Population balance modeling: current status and future prospects[J]. Annual review of chemical and biomolecular engineering, 2014, 5: 123-146.
4. Metta N, Ierapetritou M, Ramachandran R. A multiscale DEM-PBM approach for a continuous comilling process using a mechanistically developed breakage kernel[J]. Chemical Engineering Science, 2018, 178: 211-221.
5. Rogers A, Ierapetritou M G. Discrete element reduced?order modeling of dynamic particulate systems[J]. AIChE Journal, 2014, 60(9): 3184-3194.
6. Boukouvala F, Muzzio F J, Ierapetritou M G. Dynamic data-driven modeling of pharmaceutical processes[J]. Industrial & Engineering Chemistry Research, 2011, 50(11): 6743-6754.
7. Boukouvala F, Muzzio F J, Ierapetritou M G. Design space of pharmaceutical processes using data-driven-based methods[J]. Journal of Pharmaceutical Innovation, 2010, 5(3): 119-137.
8. Wang Z, Ierapetritou M. A novel feasibility analysis method for black?box processes using a radial basis function adaptive sampling approach[J]. AIChE Journal, 2017, 63(2): 532-550.
9. Wang Z, Escotet-Espinoza M S, Ierapetritou M. Process analysis and optimization of continuous pharmaceutical manufacturing using flowsheet models[J]. Computers & Chemical Engineering, 2017, 17: 77-91
10. Saltelli A, Ratto M, Andres T, et al. Global sensitivity analysis: the primer[M]. John Wiley & Sons, 2008.
11. Lawrence X Y. Pharmaceutical quality by design: product and process development, understanding, and control[J]. Pharmaceutical research, 2008, 25(4): 781-791.
Zilong Wang is currently a PhD candidate in the Department of Chemical and Biochemical Engineering at Rutgers University. He got his Bachelor’s degree from Dalian University of Technology (Dalian, China) in 2012 and his Master degree from Carnegie Mellon University (Pittsburgh, PA) in 2013. His research interests include modelling for continuous pharmaceutical manufacturing processes, applying the sensitivity and feasibility analysis to the simulationbased process development, and investigating surrogate-based methods for optimization under uncertainty.
Marianthi Ierapetritou is a Distinguished Professor and the chair at the Department of Chemical and Biochemical Engineering at Rutgers University in Piscataway, New Jersey. She completed her Bachelor’s study at National Technical University (Athens, Greece), and obtained her PhD degree from Imperial College (London, UK) in 1995. She did her post-doctoral research at Princeton University (Princeton, NJ) and then joined Rutgers University in 1998. Her research is focused on scheduling, planning, and supply chain management; uncertainty analysis; modelling and optimization of pharmaceutical and biopharmaceutical processes and biomass conversion technologies.
